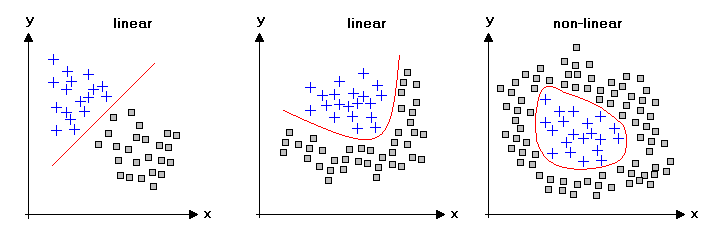
A linear regression model predicts outcomes using a straight-line relationship between variables. A nonlinear regression model uses a curved relationship.
Linear and nonlinear regression models are essential in statistical analysis and machine learning. They help predict outcomes based on input variables. Linear regression uses a simple straight-line approach. It is easy to interpret and implement. Nonlinear regression, on the other hand, uses more complex curves.
This allows for modeling more intricate relationships. Both models have their own strengths and use-cases. Linear models work best when relationships are simple and direct. Nonlinear models are better for complex, real-world data. Understanding the differences helps in choosing the right model for your data. This ensures accurate and reliable predictions.
Linear Vs Nonlinear Regression: The Basics
Linear models predict outcomes using a straight line. Nonlinear models use curved lines for predictions. Linear models have constant slopes. Nonlinear models have variable slopes. Linear models are simpler to understand. Nonlinear models can be more complex. Linear models work well with simple data. Nonlinear models handle complex data better.
Regression analysis finds relationships between variables. It uses independent variables to predict dependent variables. Linear regression fits a straight line to data points. Nonlinear regression fits a curve to data points. Both types help in forecasting and decision making. Linear regression is easier to interpret. Nonlinear regression can capture more complex patterns.
Demystifying Linear Regression
Simple linear regression predicts a response using a single feature. It finds a line that best fits the data points. This line is called the regression line. The equation is usually in the form of y = mx + c. Here, y is the response, x is the feature, m is the slope, and c is the intercept. The goal is to find the best m and c that minimize the errors. These errors are the differences between the actual and predicted values.
Multiple linear regression uses several features to predict a response. The equation is more complex than simple linear regression. It is in the form of y = b0 + b1x1 + b2x2 + … + bnxn. Here, y is the response, b0 is the intercept, and b1, b2, …, bn are the coefficients. These coefficients show the relationship between each feature and the response. The goal is to find the best b values that minimize the errors. This makes the model more accurate for real-world data.
Unraveling Nonlinear Regression
Nonlinear models are complex. They can capture curved relationships. These models do not form a straight line. They can fit data points better than linear models. Nonlinear models are used when data shows patterns. These patterns are not straight. They can predict more accurate results. Nonlinear models can adapt to different shapes. This makes them very flexible. They require more computational power.
| Type | Description |
|---|---|
| Polynomial Regression | Uses polynomials to model the data. Can fit curves of various degrees. |
| Logistic Regression | Models binary outcomes. Used in classification tasks. |
| Exponential Regression | Models data that grows or decays exponentially. |
| Power Regression | Uses a power function to fit the data. Suitable for data with power law relationships. |
Comparative Analysis: Linear Vs Nonlinear
Linear regression finds a straight line that best fits the data. Nonlinear regression fits data with a curve. Linear models are simpler and faster. Nonlinear models handle complex data patterns better. Both models predict outcomes based on input variables. Both require training data to learn patterns. Linear regression uses one equation. Nonlinear regression uses multiple equations. Linear models are easy to understand. Nonlinear models are more flexible. Linear models assume a constant relationship. Nonlinear models do not. Both methods have their pros and cons.
Choose linear models for simpler problems. Use nonlinear models for complex patterns. Linear regression works well with fewer variables. Nonlinear regression handles many variables better. Linear models are faster to compute. Nonlinear models may need more time. Consider the nature of your data. Simple data fits better with linear models. Complex or curved data fits better with nonlinear models. Analyze your data before choosing. Test both models if unsure. Choose the one that gives better results.
Real-world Applications
Linear regression predicts house prices. It looks at the number of rooms and the area. Another use is in sales forecasting. It helps businesses plan for the future. Medical researchers use it to find links between exercise and health. Linear regression is easy to understand. It is useful when the relationship is straight and clear.
Nonlinear regression is used in climate models. It helps predict weather patterns. Economists use it to study market trends. Nonlinear regression handles complex data. It finds patterns in biological systems like population growth. This model is helpful when the relationship is curved or complicated.
Credit: www.statistics4u.com
Assumptions And Limitations
Linear models assume a straight-line relationship between variables. The independent variables should be uncorrelated. Errors are normally distributed and have a constant variance. The model should not have outliers. Multicollinearity should be minimal. The data should not show autocorrelation. Assumptions help in making the model reliable.
Nonlinear regression can be complex. Finding the right model is hard. It may require iterative methods to fit the data. Initial guesses are important. Convergence to a solution is not always guaranteed. The model may overfit the data. Computational cost can be high. Nonlinear models often need more data for accuracy.
Improving Model Accuracy
Use feature scaling to improve model performance. Remove outliers to make the model more accurate. Feature selection helps in choosing the right variables. Regularization techniques like Lasso can reduce overfitting. Cross-validation ensures the model works well on new data. Adding interaction terms can capture complex relationships. Polynomial features can make the model capture curves better. Check residual plots to find patterns not captured by the model.
Kernel methods in support vector machines can handle nonlinear data. Neural networks can capture complex patterns. Boosting algorithms like AdaBoost improve accuracy. Hyperparameter tuning optimizes model performance. Data augmentation increases the dataset size. Regularization helps avoid overfitting. Choosing the right activation function in neural networks is crucial. Ensemble methods combine multiple models for better results.
:max_bytes(150000):strip_icc()/Nonlinear-regression_final-eb6cf9f18e794d63ab4ec9363f665f6b.png)
Credit: www.investopedia.com
Future Of Regression Modeling
Data analysis is evolving quickly. New tools make it easier for everyone. Machine learning helps find patterns in data. Big data is becoming more common. Cloud computing makes data storage cheaper. Artificial intelligence is improving too. These trends are changing how we analyze data.
Linear regression is still important. Nonlinear regression is getting more popular. Neural networks are a type of nonlinear regression. They can find complex patterns. Support Vector Machines are another innovation. They work well with small data sets. These techniques help us understand data better.

Credit: www.researchgate.net
Frequently Asked Questions
What Is A Non-linear Regression Model?
A non-linear regression model captures complex relationships between variables. It uses non-linear equations to predict outcomes. This model is ideal for data with curves and bends. Non-linear regression provides more flexibility than linear models, accommodating intricate patterns in data. It’s widely used in fields like biology, finance, and engineering.
Why Is Non Linear Regression Better Than Linear Regression?
Non-linear regression captures complex relationships and patterns that linear regression cannot. It provides better accuracy for non-linear data.
What Is The Difference Between Linear And Non Linear Machine Learning Models?
Linear models assume a straight-line relationship between input and output. Non-linear models capture complex, non-linear patterns. Linear models are simpler and faster. Non-linear models handle complex data better.
How To Know If A Model Is Linear?
Check if the model’s equation can be written as a linear combination of its parameters. Verify if the relationship between variables is a straight line.
Conclusion
Choosing between linear and nonlinear regression depends on your data and desired outcomes. Linear models work well for simpler relationships. Nonlinear models capture complex patterns. Understanding both helps in selecting the right approach. The correct model ensures better predictions, improving decision-making and insights.
Explore both to maximize your data’s potential.